Cara Mencari Median Data Kelompok – Mencari median data kelompok merupakan keterampilan penting dalam statistik, memungkinkan kita mengidentifikasi nilai tengah data dengan mudah. Dalam artikel ini, kita akan menyelami konsep median, menjelajahi metode manual dan kalkulator untuk menghitungnya, serta mengeksplorasi aplikasinya dalam statistik.
Table of Contents
Median, berbeda dengan mean dan modus, memberikan representasi nilai tengah yang lebih stabil, terutama saat berhadapan dengan data yang terdistribusi tidak simetris atau memiliki outlier.
Definisi dan Konsep Median
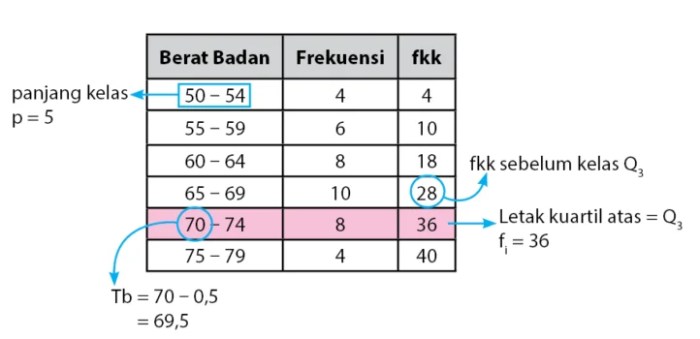
Median adalah nilai tengah dalam suatu kumpulan data yang telah diurutkan dari nilai terkecil ke terbesar. Berbeda dengan mean (rata-rata) yang memperhitungkan semua nilai data, median tidak terpengaruh oleh nilai ekstrem atau pencilan (outlier).
Median memberikan gambaran yang lebih representatif tentang nilai rata-rata suatu kumpulan data dibandingkan mean, terutama jika terdapat pencilan. Sebagai contoh, jika suatu kelas memiliki 10 siswa dengan nilai ujian sebagai berikut: 80, 85, 90, 92, 95, 97, 98, 100, 105, dan 110, maka mediannya adalah 95, sedangkan meannya adalah 95,2. Median menunjukkan bahwa sebagian besar siswa berada di kisaran nilai 90-100, sementara mean dipengaruhi oleh nilai ekstrem 110.
Jenis-jenis Median
Terdapat dua jenis median:
- Median Ganjil:Jika jumlah data ganjil, maka median adalah nilai tengah setelah diurutkan.
- Median Genap:Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengah setelah diurutkan.
Cara Mencari Median
Untuk mencari median, ikuti langkah-langkah berikut:
- Urutkan data dari nilai terkecil ke terbesar.
- Jika jumlah data ganjil, maka median adalah nilai tengah.
- Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengah.
Cara Mencari Median Secara Manual

Median adalah nilai tengah dalam suatu kelompok data yang diurutkan. Berikut cara mencari median secara manual:
Mengurutkan Data
Susun data dalam urutan dari terkecil ke terbesar. Ini akan membantu Anda menemukan titik tengah dengan mudah.
Menemukan Titik Tengah
Tentukan titik tengah data. Jika jumlah data ganjil, titik tengah adalah nilai tengah. Jika jumlah data genap, titik tengah adalah rata-rata dari dua nilai tengah.
Mencari Median
- Jika titik tengah genap, median adalah rata-rata dari dua nilai tengah.
- Jika titik tengah ganjil, median adalah nilai tengah.
Contoh
Misalkan kita memiliki data berikut: 5, 7, 9, 11, 13, 15, 17
Setelah diurutkan, data menjadi: 5, 7, 9, 11, 13, 15, 17
Karena jumlah data ganjil, titik tengah adalah nilai tengah, yaitu 11.
Jadi, median data tersebut adalah 11.
Cara Mencari Median Menggunakan Kalkulator
Menggunakan kalkulator adalah metode yang mudah dan cepat untuk mencari median data kelompok. Kalkulator memiliki fitur khusus yang dapat menghitung median secara otomatis.
Langkah-Langkah Penggunaan Kalkulator
- Masukkan data kelompok ke dalam kalkulator, baik secara manual atau melalui fungsi input data.
- Cari fitur median pada kalkulator. Biasanya ditandai dengan simbol “M” atau “MED”.
- Pilih fitur median dan kalkulator akan secara otomatis menghitung dan menampilkan nilai median.
Setelah mengikuti langkah-langkah ini, kalkulator akan memberikan nilai median data kelompok yang dimasukkan.
Aplikasi Median dalam Statistik
Median adalah ukuran statistik yang banyak digunakan untuk mewakili nilai tengah suatu kumpulan data. Median memiliki beberapa keunggulan dan keterbatasan dalam analisis data.
Keunggulan Median
- Median tidak terpengaruh oleh nilai ekstrem (outlier).
- Median mudah dihitung, bahkan untuk kumpulan data yang besar.
- Median dapat digunakan untuk membandingkan kumpulan data yang memiliki skala pengukuran berbeda.
Keterbatasan Median, Cara Mencari Median Data Kelompok
- Median tidak memberikan informasi tentang penyebaran data.
- Median tidak dapat digunakan untuk menghitung statistik lain, seperti mean atau standar deviasi.
- Median tidak sepeka terhadap perubahan data seperti mean.
Median dapat menjadi ukuran statistik yang berguna dalam situasi berikut:
- Ketika data terdistribusi tidak simetris.
- Ketika terdapat nilai ekstrem dalam data.
- Ketika ingin membandingkan kumpulan data yang berbeda.
Tips dan Pertimbangan

Mencari median data kelompok melibatkan beberapa faktor dan pertimbangan penting. Memahami faktor-faktor ini dapat membantu Anda menghindari kesalahan umum dan memperoleh nilai median yang akurat.
Jumlah Data
Jumlah data dalam kelompok dapat memengaruhi nilai median. Ketika jumlah data genap, median adalah rata-rata dari dua nilai tengah. Jika jumlah data ganjil, median adalah nilai tengah. Jumlah data yang lebih besar biasanya menghasilkan nilai median yang lebih stabil dan representatif.
Outlier
Outlier adalah nilai yang sangat berbeda dari nilai lainnya dalam kelompok data. Outlier dapat memengaruhi nilai median, terutama ketika jumlah datanya kecil. Dalam kasus seperti itu, mempertimbangkan median yang dipangkas atau median Winsorized dapat membantu mengurangi pengaruh outlier.
Kesalahan Umum
Berikut adalah beberapa kesalahan umum yang harus dihindari saat mencari median:
- Menghitung rata-rata sebagai ganti median
- Tidak mengurutkan data sebelum mencari median
- Tidak mempertimbangkan outlier saat jumlah data kecil
- Menggunakan rumus median yang salah
Kelebihan dan Kekurangan Median
| Kelebihan | Kekurangan |
|---|---|
| Tidak terpengaruh oleh outlier | Tidak memberikan informasi tentang distribusi data |
| Mudah dihitung | Kurang tepat dibandingkan rata-rata dalam beberapa kasus |
| Lebih representatif untuk data yang tidak normal | Dapat terpengaruh oleh jumlah data yang genap |
Penutupan: Cara Mencari Median Data Kelompok
Memahami cara mencari median data kelompok memberdayakan kita untuk menganalisis dan menginterpretasikan data secara efektif. Dengan menggunakan metode yang diuraikan dalam artikel ini, kita dapat memperoleh wawasan berharga dari kumpulan data, membuat keputusan yang lebih tepat, dan mengomunikasikan temuan kita dengan jelas.
FAQ Terkini
Apa perbedaan antara median, mean, dan modus?
Median adalah nilai tengah data, mean adalah rata-rata aritmatika, dan modus adalah nilai yang paling sering muncul.
Kapan sebaiknya saya menggunakan median daripada mean?
Median lebih tepat digunakan ketika data terdistribusi tidak simetris atau memiliki outlier, karena tidak dipengaruhi oleh nilai ekstrem.
Tags: